Introduction to Tensorflow
TensorFlow is a powerful machine learning library created by the Brain Team of Google and made open source in 2015. It is designed for easy usage and widely applicable to both numeric and neural network-oriented problems as well as other domains. Basically, we can say that TensorFlow is a low-level toolkit for doing complicated math which ultimately targets researchers who are building experiential machine learning models and turn them into running software.
Many of the world’s toughest scientific challenges, like developing high-temperature superconductors and understanding the true nature of space and time involved dealing with the complexity of quantum systems. The number of quantum states in these systems is exponentially large is a more challenging task, which makes brute-force computation infeasible. To deal with this, data structures called tensor networks are used. Tensor networks focus on the quantum states that are most relevant for real-world problems the states of low energy, say while ignoring other states that aren’t relevant. Tensor networks are increasingly finding applications in machine learning.
In order to address these issues, we are releasing TensorNetwork, a brand new open-source library to improve the efficiency of tensor calculations, developed in collaboration with the Perimeter Institute for Theoretical Physics and X. TensorNetwork uses TensorFlow as a backend and is optimized for GPU processing, which can enable speedups of up to 100x when compared to work on a CPU.
How are Tensor Networks Useful?
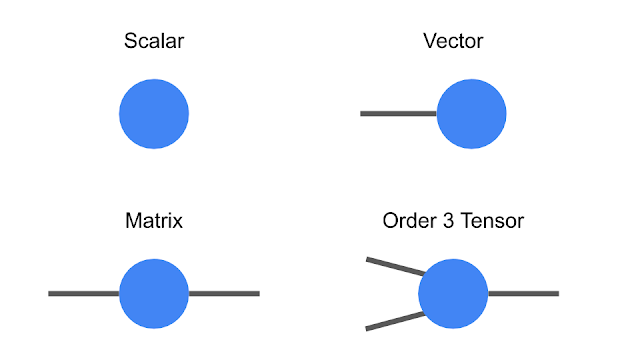
Tensors are multidimensional arrays, categorized in a hierarchy according to their order. e.g., an ordinary number is a tensor of order zero which is also known as a scalar, a vector is an order-one tensor, a matrix is an order-two tensor, and so on. While low-order tensors can easily be represented by an explicit array of numbers or with a mathematical symbol such as T where the number of indices represents the order of tensor, that notation becomes very cumbersome once we start talking about high-order tensors. At this point it’s useful to start using diagrammatic notation, where one can simply draw a circle or some other shape with a number of lines, or legs, coming out of it the number of legs being the same as the order of the tensor. As the scalar is just a circle, a vector has a single leg, a matrix has two legs, etc. Consider a vector representing an object’s velocity through space would be a three-dimensional, order-one tensor.
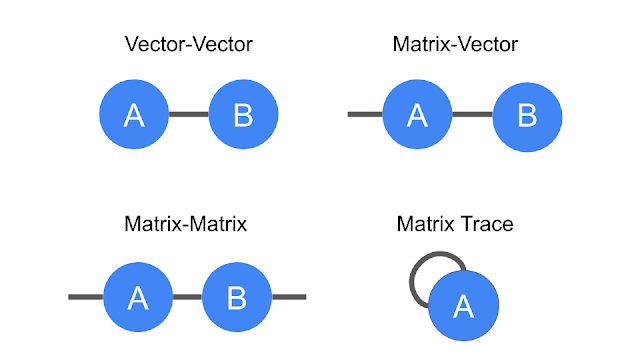
The benefit of representing tensors in this way is to encode mathematical operations, e.g., multiplying a matrix by a vector to produce another vector, or multiplying two vectors to make a scalar. These are generally referred to as tensor contractions.
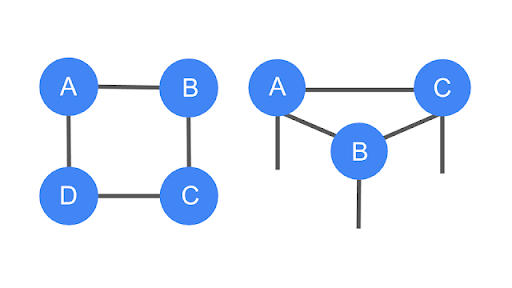
These are examples of tensor networks, which are graphical ways of encoding the pattern of tensor contractions of several constituent tensors to form a new one. Each constituent of tensor has an order determined by its own number of legs. Legs that are connected, forming an edge in the diagram, represent contraction, while the number of remaining dangling legs determines the order of the resultant tensor. The trace of the product of four matrices, tr(ABCD), which is a scalar. You can see that it has no dangling legs.
Tensor Networks in Practice
Considering a collection of black-and-white images, each of which can be thought of as a list of N pixel values. A single pixel of a single image can be one-hot-encoded into a two-dimensional vector, and by combining these pixel encodings together we can make a 2N-dimensional one-hot encoding of the entire image. We can reshape that high-dimensional vector into an order-N tensor, and then add up all of the tensors in our collection of images to get a total tensor encapsulating the collection.
This sounds like a very wasteful thing to do: encoding images with about 50 pixels in this way would take petabytes of memory. That’s where tensor networks come in. Rather than storing or manipulating the tensor T directly, we instead represent T as the contraction of many smaller constituent tensors in the shape of a tensor network. That turns out to be much more efficient. For instance, the popular matrix product state network would write T in terms of N much smaller tensors, so that the total number of parameters is only linear in N, rather than exponential.
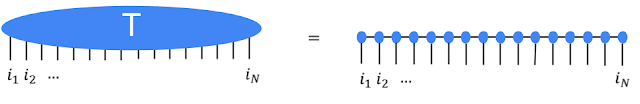
The high-order tensor T is represented in terms of many low-order tensors in a matrix product state tensor network. It’s not obvious that large tensor networks can be efficiently created or manipulated while consistently avoiding the need for a huge amount of memory. But it turns out that this is possible in many cases, which is why tensor networks have been used extensively in quantum physics and, now, in machine learning. Stoudenmire and Schwab used the encoding just described to make an image classification model, demonstrating a new use for tensor networks.
Performance in Physics Use-Cases
Tensor Networks are the general-purpose library for tensor network algorithms, and so it should prove useful for physicists as well. Approximating quantum states is a typical use-case for tensor networks in physics, and is well-suited to illustrate the capabilities of the TensorNetwork library. We compare the use of CPUs with GPUs and observe significant computational speed-ups, up to a factor of 100, when using a GPU and the TensorNetwork library.