What is KMEANS Unsupervised Learning Algorithm?

28 July 2021

Before we deep dive into KMeans algorithm first we need to understand what clustering is. So,

What is Clustering?

• Clustering is an unsupervised learning technique.
• It is the task of grouping a set of objects in such a way that objects in the same group(cluster) are more similar to each other than to those in other groups.

Various algorithms are:

• KMEANS clustering.
• Hierarchical Clustering.
• Density Based Spatial Clustering of Applications with Noise (DBSCAN).
• Expectation – Maximization algorithm.

KMeans Clustering Algorithm

• In KMEANS we try to group the people or group the observation based on the similarity and the similarity is measured using the distance and the distance used is Euclidean distance.
• KMeans is a non-deterministic algorithm. Why non-deterministic? This is because our output is not fixed even when our input data is fixed and all the processing steps are fixed, our output may slightly change everytime we run our KMeans algorithm.
• In KMEANS clustering, the given data points are grouped into K clusters, based on the similarity of the data points.

Now, there may be a doubt that how to select K in KMeans

Elbow Method: In Elbow method or Elbow plot, on our x-axis we have number of clusters and on y-axis we have sum squared distance or also called sum squared error for each number of clusters and wherever we see a sudden drop we take that cluster as an optimum number of clusters.

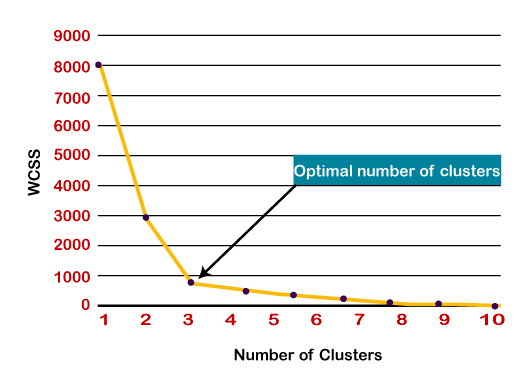
Here, from the above elbow plot figure, we can see that there is a sudden drop (bend) in 3. Hence our optimal number of clusters (K) will be 3.

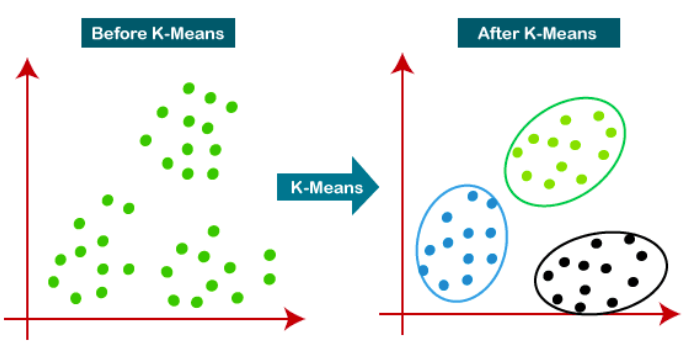
Algorithm:

Step 1: Randomly select k cluster centers vi…..vk.

Step 2: Calculate the distance between each data point aj and each cluster   centers vi

Step 3: Assign each data point aj to the cluster centre vi for which the distance

|| aj-vi|| is minimum.

Step 4: Recalculate each cluster center by taking the average of cluster’s data points.

Step 5: Repeat from step 2 to step 4 until the recalculated cluster centers are same as previous or no reassignment of data points happened

Distance between data points:

Let’s assume that each data point is a  n-dimensional vector.

The distance between two data points:

x=(x1…….xn)

and 

y=(y1............yn)

Is defined as

||x-y||=(x1-y1)2+.............(xn-yn)2